1. PCA算法
1.1 PCA的数学原理
转载: PCA的数学原理
PCA的算法步骤:
设有m条n维数据。
1)将原始数据按列组成n行m列矩阵X
2)将X的每一行(代表一个属性字段)进行零均值化,即减去这一行的均值
3)求出协方差矩阵 $$C=1/mXX^T$$
4)求出协方差矩阵的特征值及对应的特征向量
5)将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P
6) Y=PX 即为降维到k维后的数据
1.2 主成分分析(PCA)原理及推导
Tips:
a. A与B的内积等于A到B的投影长度乘以B的模。
b.两个矩阵相乘的意义是将右边矩阵中的每一列列向量变换到左边矩阵中每一行行向量为基所表示的空间中去 。更抽象的说,一个矩阵可以表示一种线性变换。
2. SVD
Tips:
a. SVD分解公式: $$M = U Σ V^T$$
这表明任意的矩阵 M 是可以分解成三个矩阵。 V 表示了原始域的标准正交基, u 表示经过 M 变换后的co-domain的标准正交基,
Σ 表示了 V 中的向量与 u 中相对应向量之间的关系。
3. PCA与SVD之间的关系
机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用
Tips:
a. 特征值分解是一个提取矩阵特征很不错的方法,但是它只是对方阵而言的,对于普通矩阵,只能用SVD。
b. PCA几乎可以说是对SVD的一个包装,如果我们实现了SVD,那也就实现了PCA了,而且更好的地方是,有了SVD,我们就可以得到两个方向的PCA,如果
我们对A’A进行特征值的分解,只能得到一个方向的PCA。
c.SVD分解基本方法:
我们将一个矩阵A的转置 * A,将会得到一个方阵,我们用这个方阵求特征值可以得到:
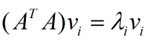
这里得到的v,就是我们上面的右奇异向量。此外我们还可以得到:
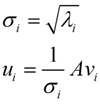
这里的σ就是上面说的奇异值,u就是上面说的左奇异向量。奇异值σ跟特征值类似,在矩阵Σ中也是从大到小排列,而且σ的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了 。也就是说,我们也可以用前r大的奇异值来近似描述矩阵,这里定义一下部分奇异值分解 :
